The Facts About Multiplication Facts

As some of you may know, Ontario released a new math curriculum in 2020. There are a few new strands, such as financial literacy and coding, but one major philosophical change is the requirement for students to memorize their multiplication facts. In grade 5, students are required to learn their facts up to 12 x 12.

I have written about memorizing facts before, and have participated in workshops on online webinars to learn other strategies for helping students learn their facts. I personally believe that there is a balance between memorizing and learning the “why” of multiplication. I don’t believe it’s an all or nothing, you just know them or you don’t, kind of thing. There may be some facts that come more easily, and others that are more difficult. Using strategies to make those more difficult ones make sense seems so much more beneficial than simply just memorizing it.

With all that being said, the one common strategy, whether you are learning or memorizing, is practice! Talk about multiplication, think about multiplication, practice multiplication, make it a part of your daily routine, and it will get easier! Therefore, over the next number of weeks, in addition to reading daily, students will be required to practice their multiplication facts until they are mastered. Some may already be there, some may need until the end of the year. Either way is perfect! Students will have the opportunity to demonstrate their mastery whenever they are ready, fact by fact.

Think About Multiplication

I highly recommend watching this webinar (it’s about an hour long) for some ideas about how you can talk about the facts to help your child learn those trickier ones.

Read About Multiplication

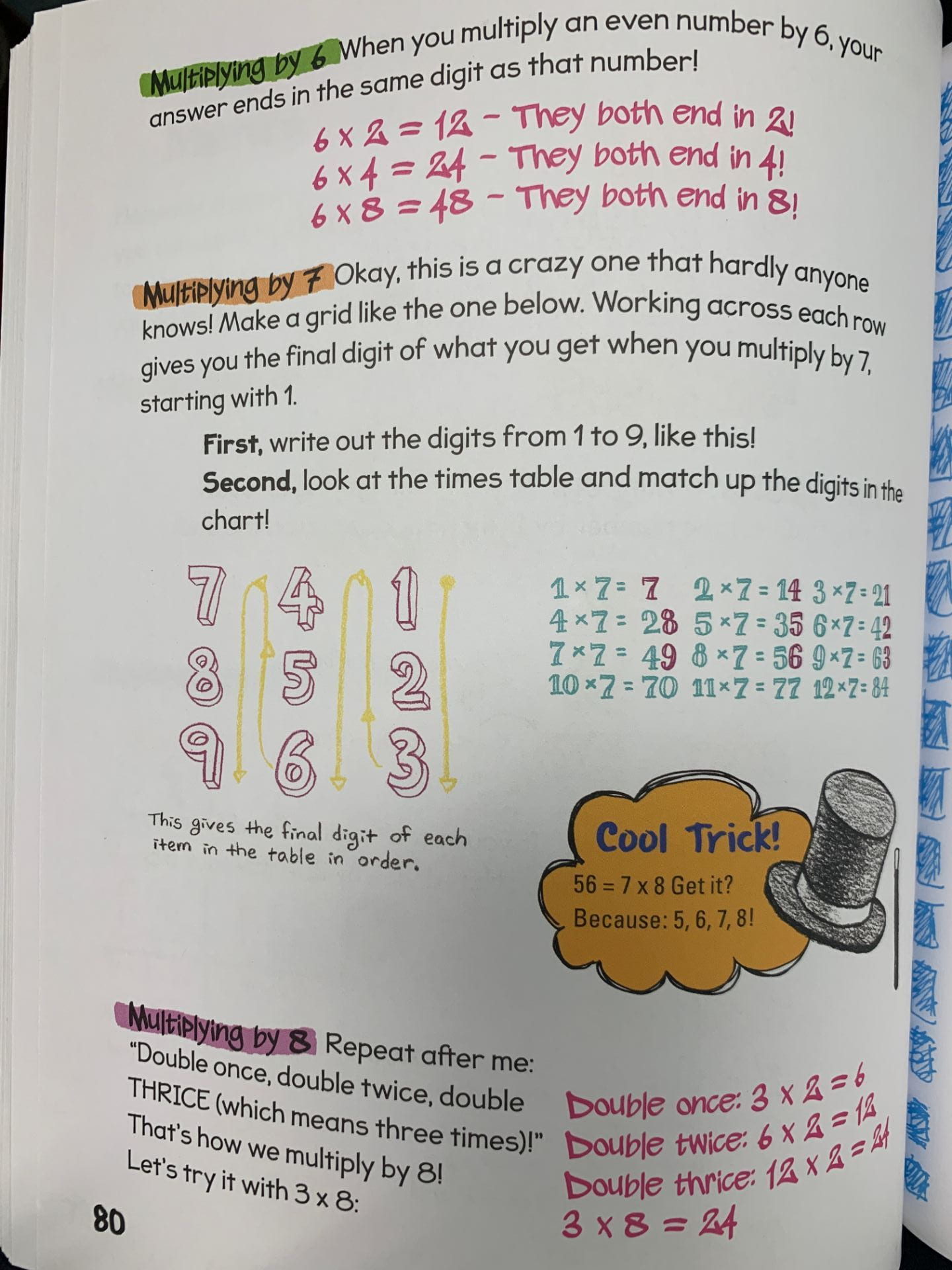
Here are some strategies from a book I got at the Scholastic Book Fair two years ago, Math Hacks by Vanessa Vakharia (if you follow the link, there are some suggestions for online sites and games for practice)

This slideshow requires JavaScript.

Practice Multiplication

Make Flashcards. This is much better than buying them premade! Writing the facts down is in itself a form of practice. Students can cut the cards, write the multiplication sentence on one side, and the answer on the back.
Math rap songs. For our auditory learners, listening to songs about multiplication and adding a beat to it can be helpful. Students can learn all the newest pop songs by heart…why not their multiplication facts? YouTube has tons of options. You just need to find the one that appeals to you. Here’s a site with 30 fun ideas that play on your musical, artistic, or kinesthetic learning style.
Online multiplication practice. These are a few suggestions but there are TONS to choose from.
Printed practice sheets. I have heaps of practice sheets that students can take home.
Find tricks to help you remember your facts.
Mrs. Cleveland has also created a list on her math blog, to many different useful math practice sites, not only just for multiplication.

Taking too long?

Reload document

Open in new tab

Download

If you have any questions or comments, we’d love to hear from you! Happy multiplying!

Category: 5A, 5B, Homework, Math | 3 Comments

March 22

Multiplication Practice at Home

I little while back I wrote this post about whether or not we should be memorizing our facts. The verdict is still out, however my own opinion is that I don’t believe memorization is the best strategy. But, I do think that it is extremely important to practice! I gave a few suggestions for practicing your facts at home in that post, however, while we are learning from home over the next few weeks, and especially while we are in our Multiplication and Division unit in math, practicing at home will be very important. Here are a few different ways to practice.

TheDigitalArtist / Pixabay

Here’s a site with 30 fun ideas that play on your musical, artistic, or kinesthetic learning style.

This site has a few different activities for each fact to help practice (and memorize if you believe in that)

Mrs. Cleveland has also created a list on her math blog, to many different useful math practice sites, not only just for multiplication.

Taking too long?

Reload document

Open in new tab

Download

Category: Math | LEAVE A COMMENT

January 17

To Memorize, or Not to Memorize?

When it comes to multiplication facts, I’ve often heard…you just need to memorize them.

Over the years, I’ve had students who knew their facts backwards and forwards, and others who just couldn’t remember them. It has always been my goal to find ways to help my students learn their facts. Should I be giving time to just practice and memorize in class? Should I teach them different tricks for each set of numbers? Is there another way I don’t know about?

In May 2019 I attended the OAME (Ontario Association for Mathematics Education) Conference here in Ottawa, and focused my sessions around building better fluency. One session I attended, led by Melissa Peddie, Chrissy Chabot, and Laurie Clayton, said that true fluency happens when three things are present: Efficiency, Accuracy, and Flexibility.

Repeated addition, or skip counting, is a great strategy to use when we are first learning multiplication, but these presenters believed that come grade 4, students should no longer be using skip counting as a strategy. We really want students to think about what they are doing, and how numbers relate to each other. “Add a zero” when multiplying by ten is a common trick students are taught. Let’s look at an example and put it through the fluency test.

12.2 x 10

If students were thinking of the trick they had been taught, they would simply add a zero to the end for a solution of 12.20

Hopefully, all my grade 5 students can tell you that 1) 12.2 and 12.20 are equivalent decimals and 2) this is not how you multiply a decimal by 10. Therefore, was the strategy efficient? Yes, I got an answer pretty quickly. Was it accurate? No, I did not get the correct answer. And was it flexible? It wasn’t, because the strategy only works for whole numbers.

Pam Harris, from mathisfigureoutable.com shares the opinion that multiplication facts should be thought about, rather than memorized. I recently attended one of her Facebook Live webinars (I highly recommend watching this recorded version, it’s about an hour long), and she reiterated the importance of having students come up with strategies of their own, breaking problems into more manageable pieces, in order to come to a solution. She offers some great ways you can start helping your child learn their facts at home, by talking about doubles and halves.

In class, students will be spending 10 minutes, three times per week, working on their math facts through Strategy Kits, inspired by the session I attended at the OAME Conference. In these kits, students will make strategy cards for each of the facts they’re working on, play games, and practice with one another until they master their facts.

Some of you may still be on the fence with this and want some good ol’ strategies to help your child learn their facts.

Here are some strategies from a book I got at the Scholastic Book Fair last year, Math Hacks by Vanessa Vakharia (if you follow the link, there are some suggestions for online sites and games for practice)

I also wrote a post about strategies here and here, with links to some online practice sites.

I’d love to hear your thoughts on this. Keep talking math at home 🙂

Category: Math | 2 Comments